[1925]ナンプレ 眺めて解こう .　(2024-09-16 10:59:14)

.
tonbee様

＞「1でも1でなくても」という考え方
＞「間違った仮定からスタートした場合でも正しい結論に至ることがある」

論理学的には、間違った仮定からは（推論途中で矛盾が判明することもありますが それを無視して形式的に推論を進めれば）真偽関係なく あらゆる結論を導くことができます。

なので
「間違った仮定からスタートした場合（矛盾を無視すれば）必ず正しい結論に至ることができる」

それで
「1でも1でなくても」到達できる結論のみが「正しい結論」
となります。

[1921]tonbee　(2024-09-15 19:04:58)

眺めて解こう様
新スレッドに移るとのことですが、このコメントは私の独り言みたいなものですので ここに書きました。

9月の「私のヒント」については 一応全て理解できました。
理解できた場合は 原則ノーコメントのつもりでいます。
ただ 2021.1.1の問題のヒントについては感想を書かせていただきます。

このヒントは難解だったので、「次の一手」で正解を調べて 終点が6になることを知った上で考えました。
下(r5c9)の1からは簡単に終点6に至りました。
しかし、上の1からのルートは悩みました。
上の1を始点にすると r1c1に6が入り、終点の6を否定することになってしまったからです。
「1でも1でなくても」という考え方は、「間違った仮定からスタートした場合でも正しい結論に至ることがある」ということを利用してるんですよね。
それに納得できてから「上の1を始点にしても終点を6にできる別のルートがあるはずだ」と確信し、探してみたら r4c6に8が入るルートを見つけられ 解決できました。
この課題を通して 今まで何となく納得できていなかった問題が納得できてスッキリしました、感謝です。

ところで、私は リストで名称を知っているだけで その解説を読んだことすらないテクニックが沢山あるのですが、最近 「私のヒント」や「次の一手」が きっかけでいくつかのテクニックの解説を読んでみました。
その内の１つがフォーシング チェーンです。
読んでビックリ、これ 「1でも1でなくても」の考え方じゃないの！
無知は恐ろしいですねえ。(でも 知る喜びを得る機会は多くて面白いです)

以上、長文失礼しました。

[1918]SudokuHole　(2024-09-14 16:24:51)

数独の穴

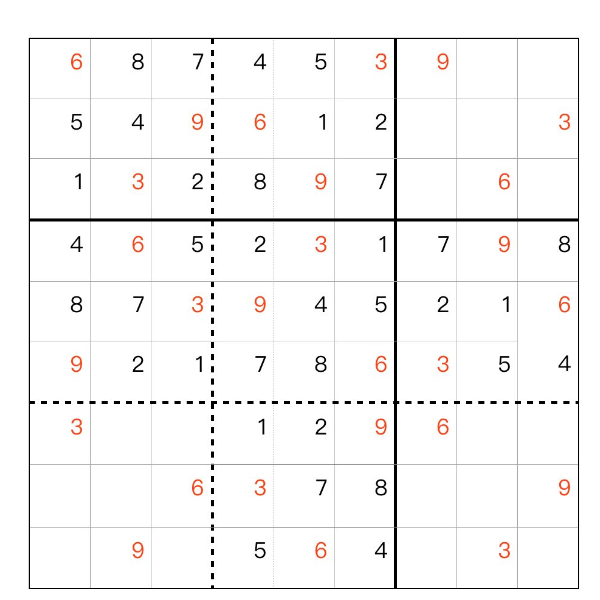
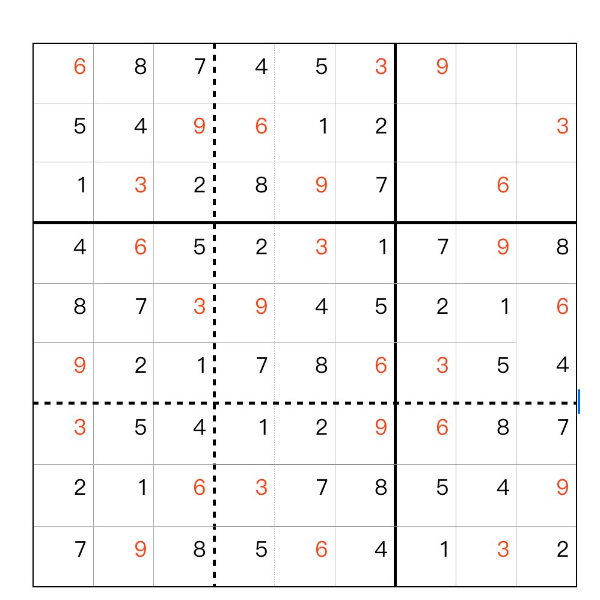
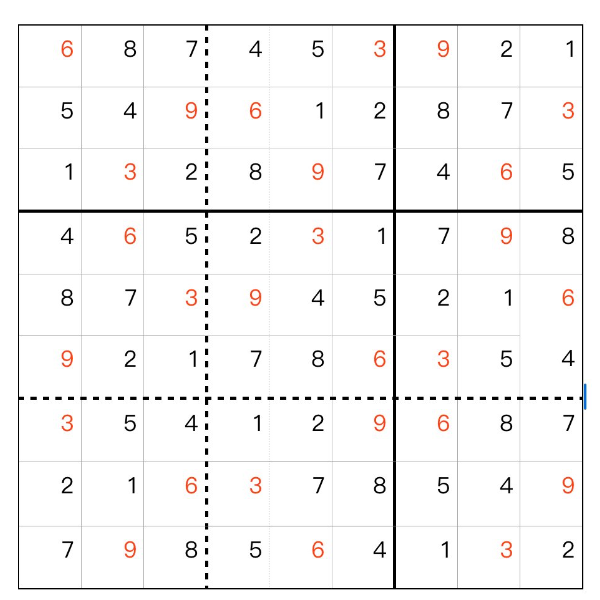
[1917]SudokuHole　(2024-09-14 16:23:53)

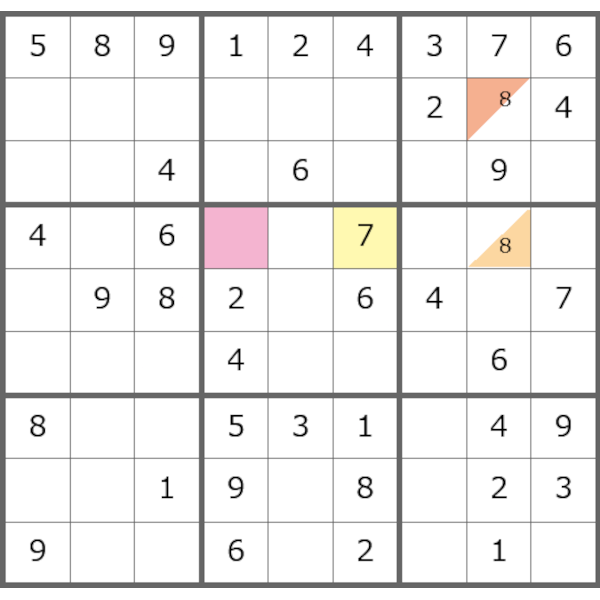
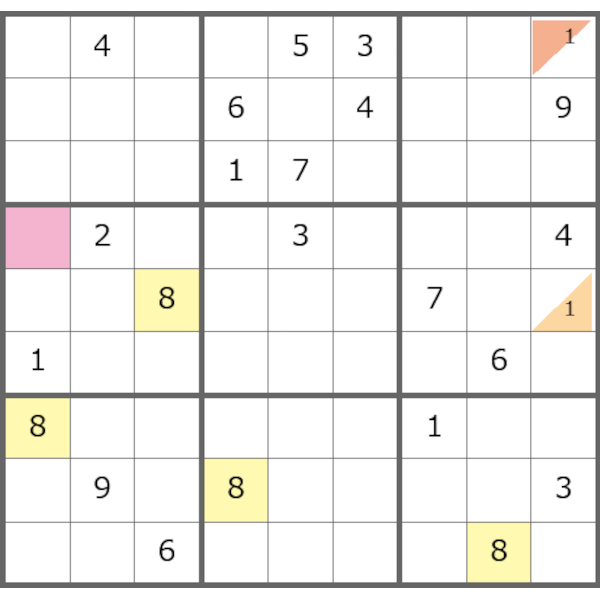
数独の穴　例題　、問題1 　、　
第一歩
第二歩
第三歩
第四歩
第五歩

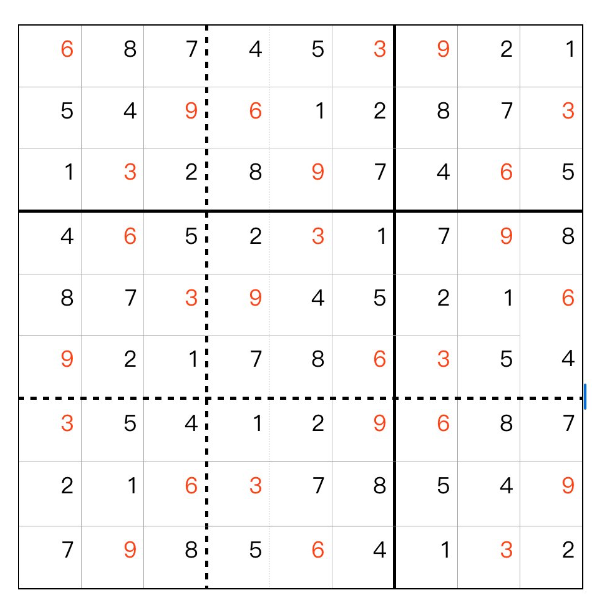
[1916]SudokuHole　(2024-09-14 16:21:15)

数独の穴　例題　、問題1 　、　第四歩

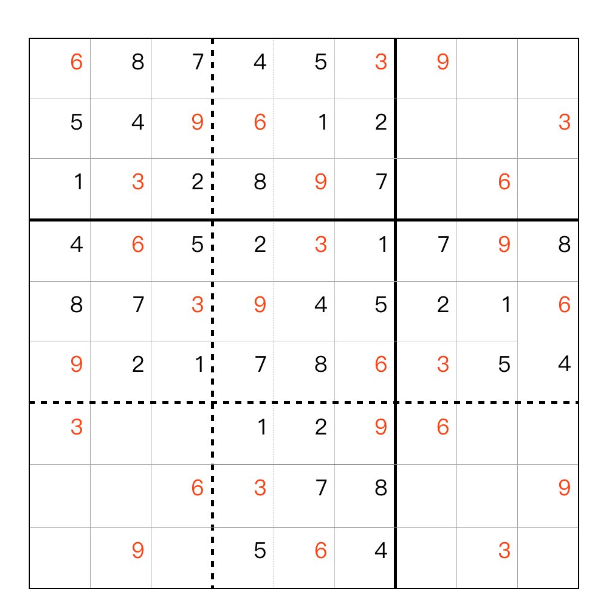
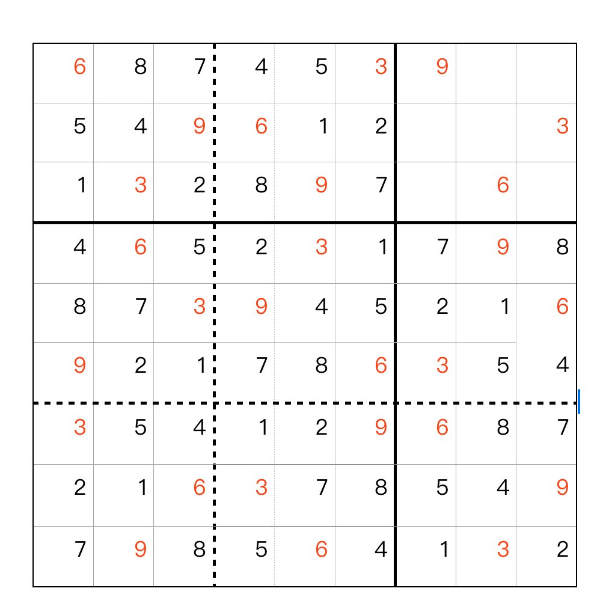
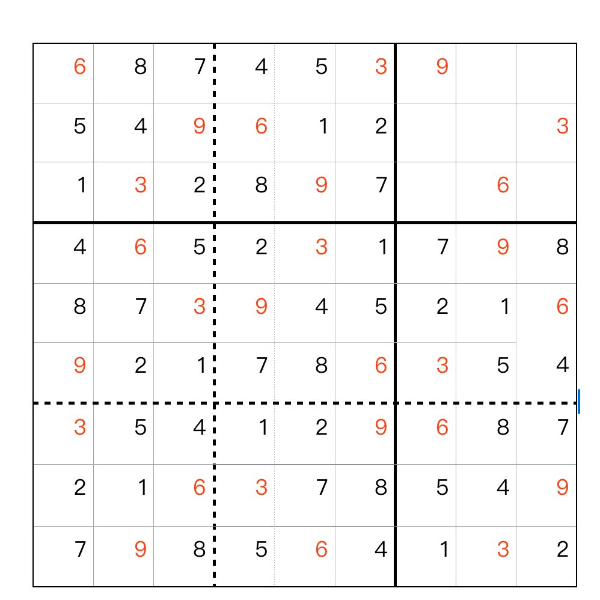
[1915]SudokuHole　(2024-09-14 16:20:22)

数独の穴　例題　、問題1 　、　第三歩

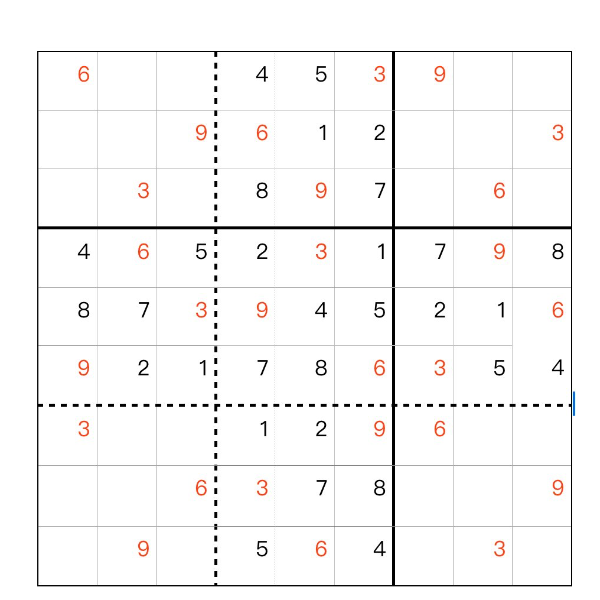
[1914]SudokuHole　(2024-09-14 16:17:38)

数独の穴　例題　、問題1 　、　第二歩

[1913]SudokuHole　(2024-09-14 16:16:58)

数独の穴　例題　、問題1 　、　第一歩

[1912]SudokuHole　(2024-09-14 16:15:45)

数独の穴　例題　、問題1
　

[1910]ナンプレ 眺めて解こう .　(2024-09-13 22:24:38)

スレッドに無関係の投稿が混ざってしまったようなので、このスレッドは改めて作り直します。

[1909]SudokuHole　(2024-09-13 20:14:49)

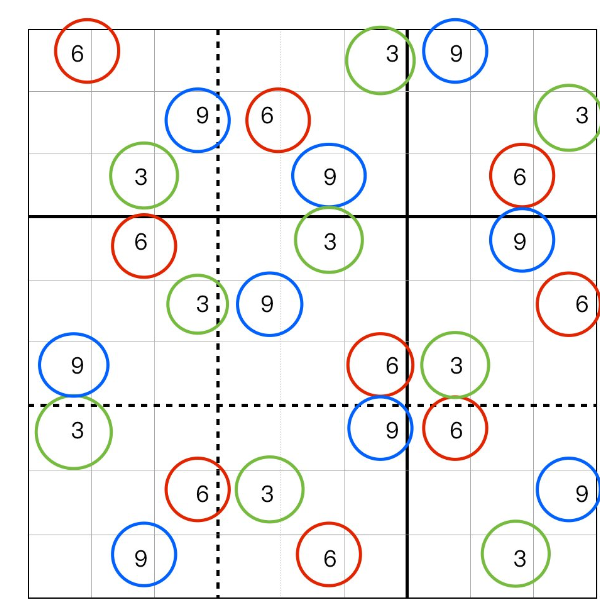
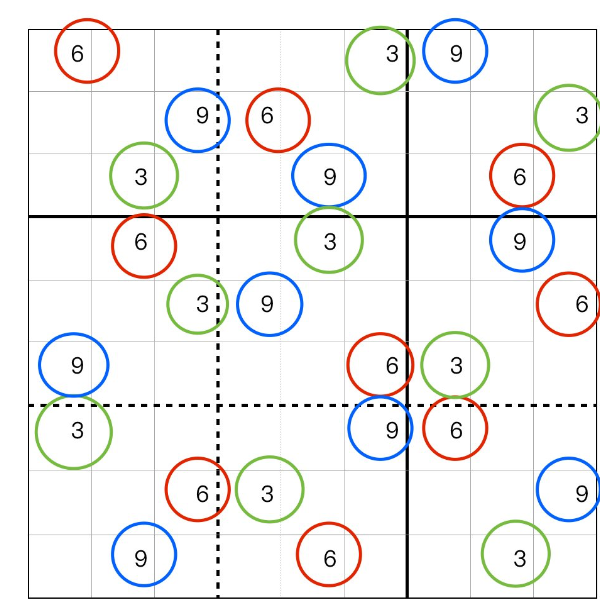
数独には、斜めの二つユニットお互いに比べると、それぞれ　同じ三組のカップル数字が、各行、あるいは各列に存在して、同じ色の絵線に示されるように見分けることができます。各行、列に見つからなくでも、二種類斜め三本線には見つかれます。例えば、中央ユニットの上下左右　二ペアの斜めユニットに、同じ三組のカップル数字が、各行、あるいは各列に存在して、同じ色の絵線の数字に見分けることができます。
ご覧ください。
これは　カップル数独と言います。

[1908]SudokuHole　(2024-09-13 20:10:29)

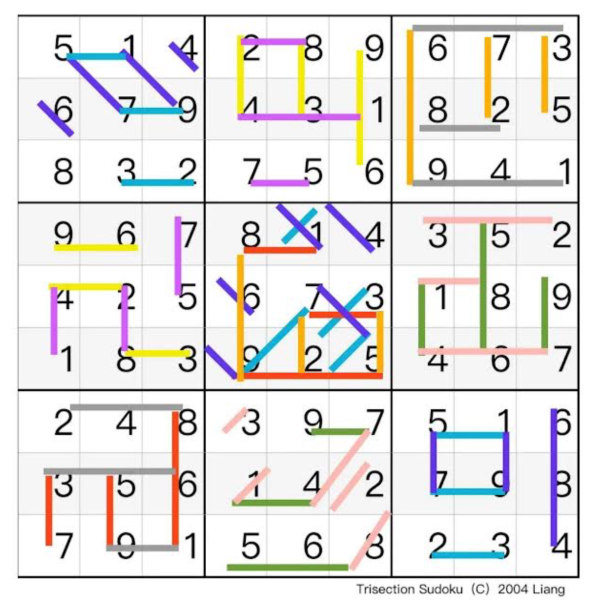
数独のアートです。面白いでしょう。考案者は僕です。一緒に研究、発表できる仲間を募集中です。21世紀の”ニコリ”
を作りたいです。数独ファンの皆様、よろしくお願いいたします。

[1907]SudokuHole　(2024-09-13 20:07:33)

子供用絵文字数独です。お試してください。元の数独数字にご覧還元してみませんか？

[1906]SudokuHole　(2024-09-13 20:05:58)

子供用絵文字数独です。お試してください。元の数独数字にご覧還元してみませんか？

[1905]SudokuHole　(2024-09-13 20:03:46)

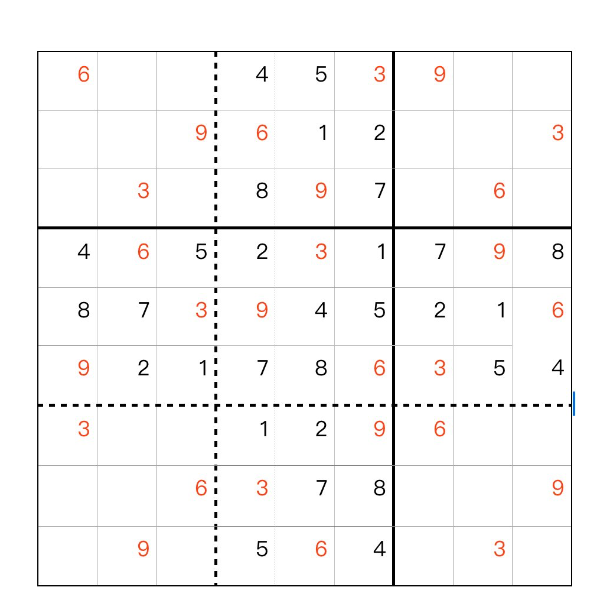
数独には、コナーの四つユニットでは、斜めの中央ユニットと比べると、それぞれ　同じ三組のカップル数字が、各行、あるいは各列に存在して、同じ色の数字に見分けることができます。各行、列に見つからなくでも、斜め三本線には見つかれます。まだ、中央ユニットの上下左右　二ペアの斜めユニットにも、同様的に、同じ三組のカップル数字が、各行、あるいは各列に存在して、同じ色の数字に見分けることができます。
ご覧ください。
これは　数不独と言います。

[1904]ナンプレ 眺めて解こう .　(2024-09-13 18:10:35)

Lv.9 2021-01-02 難易度 SE7.2

[1903]ナンプレ 眺めて解こう .　(2024-09-13 14:37:40)

Lv.9 2021-01-01 難易度 SE7.1