 文章:
文章:DTP関連のIT技術者。システム開発など
運営:嵐山デザインガレージ合同会社たけうちとおるのスクリプトノート| ファイナンシャルプランナー| 著書(Amazon)


スポンサーリンク
下図のようなパターンになった時赤色のZが候補から外されます。
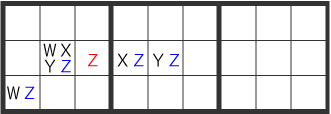
具体的には下図を見てください。[9]が全てのマスにでてきます。この[9]が[Z]です。
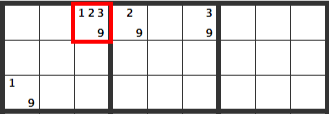
もし左下の[19]のマスが[9]ならば当然このBOXの他のマスに[9]は入りません。
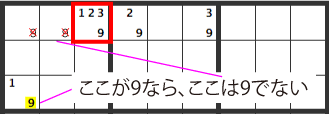
もし左下の[19]のマスが[1]ならば[9]は上の行のどこかに必ず入ることになり、同じ行の図で示した場所に[9]はやはり入りません。
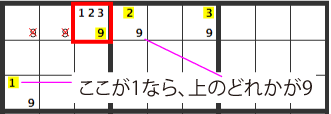
このようにWXYZ-ウイングは4つのマスと4つの候補数字の組み合わせで他のマスから候補数字を削除するテクニックです。
このパターンもWXYZ-ウイングです。どの数字?と思いますが[5]になります。検証しましょう。
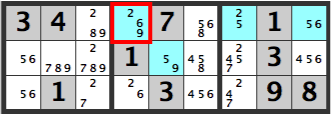
下図の中央BOX[59]マスが[5]ならば同じBOXや同じ行の[5]は候補から外されます。
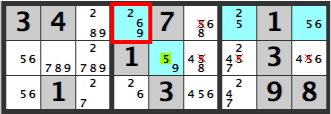
下図の中央BOX[59]マスが[9]ならば、右側のBOXの水色のマスのどちらかに5が入ります。
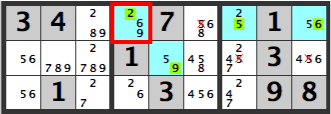
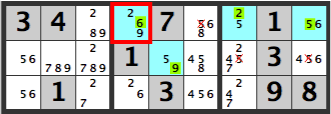
したがって共通するXが候補から除外できます
このパターンもWXYZ-ウイングです。かなりの変形パターンです。[4]が[Z]になります。検証しましょう。

下図の左BOX[14]マスが[4]ならば同じ行の[4]は候補から外されます。

下図の左BOX[14]マスが[1]ならば右BOXの水色マスが[4]になります。

したがって共通するXが候補から除外できます
また変形パターンです。いろんなパターンがあるので4つのマス、4つの数字で探した方が良さそうです。
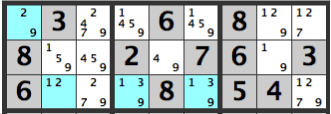
下図の左BOX[29]マスが[9]ならば同じ行の[9]は候補から外されます。
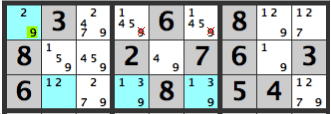
下図の左BOX[29]マスが[2]ならば中央のBOXのどちらかに[9]が入りますね。
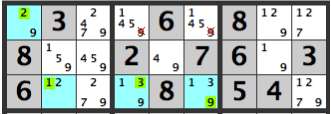
したがって共通するXが候補から除外できます
| R1C1 | R1C2 | R1C3 | R1C4 | R1C5 | R1C6 | R1C7 | R1C8 | R1C9 |
| R2C1 | R2C2 | R2C3 | R2C4 | R2C5 | R2C6 | R2C7 | R2C8 | R2C9 |
| R3C1 | R3C2 | R3C3 | R3C4 | R3C5 | R3C6 | R3C7 | R3C8 | R3C9 |
| R4C1 | R4C2 | R4C3 | R4C4 | R4C5 | R4C6 | R4C7 | R4C8 | R4C9 |
| R5C1 | R5C2 | R5C3 | R5C4 | R5C5 | R5C6 | R5C7 | R5C8 | R5C9 |
| R6C1 | R6C2 | R6C3 | R6C4 | R6C5 | R6C6 | R6C7 | R6C8 | R6C9 |
| R7C1 | R7C2 | R7C3 | R7C4 | R7C5 | R7C6 | R7C7 | R7C8 | R7C9 |
| R8C1 | R8C2 | R8C3 | R8C4 | R8C5 | R8C6 | R8C7 | R8C8 | R8C9 |
| R9C1 | R9C2 | R9C3 | R9C4 | R9C5 | R9C6 | R9C7 | R9C8 | R9C9 |
Rは行(Y軸)、Cは列(X軸)となっています。(Row、Column)
 文章:
文章:DTP関連のIT技術者。システム開発など
運営:嵐山デザインガレージ合同会社