 文章:
文章:DTP関連のIT技術者。システム開発など
運営:嵐山デザインガレージ合同会社たけうちとおるのスクリプトノート| ファイナンシャルプランナー| 著書(Amazon)


スポンサーリンク
下図のように[12]が入っているマスですが
1 2
2 1
でも
2 1
1 2
でも成り立ちます。どっちでもいいわけです。
どっちでもいいというのではナンプレの問題になりません。これが前提になります。

ちなみに[34]は入れ替わる事は出来ません。入れ替わるのが同じBOXではないので数字が入れ替わる事は出来ません。
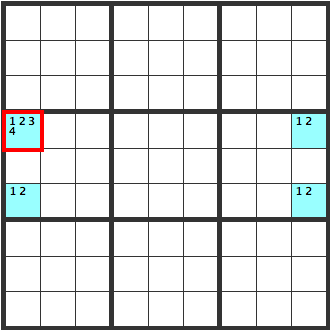
図のように[12]が入れ替わることができるパターンです。入れ替わることができればナンプレの問題として成り立たないので赤枠には[3]か[4]が入ります。
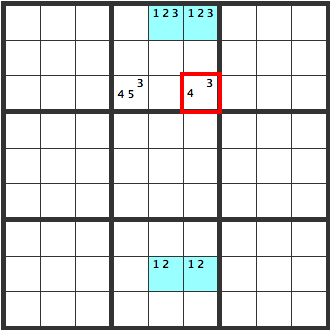
このパターンでは上の[123]の2マスのうちどちらかは必ず[3]になります。ということは赤枠には[3]は入らないので[4]になります。
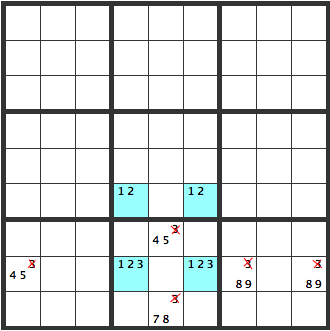
このパターンでは下の[123]の2マスのうちどちらかは必ず[3]になります。ということはBOX内の他のマスには[3]は入りません。また左右のBOXの8行も[3]は入りませんね。
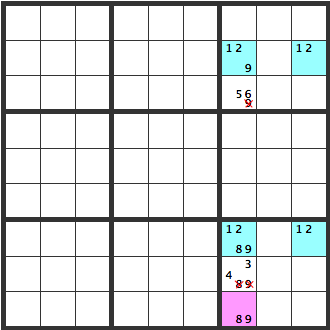
[129]のマスか[1289]のマスには[8]か[9]が必ず入ります。一番下に[89]が候補のマスがあるので上の水色のマスに[8]が入るとピンクのマスは[9]になり、水色のマスに[9]が入るとピンクのマスは[8]になるのでXの部分に[8][9]は入りません。

[128]のマスか[129]のマスには[8]か[9]が必ず入ります。ピンクのマスは[89]だけが候補になっていますので水色のマスどちらに[8]か[9]が入ったとしてもピンクのマスに[8]か[9]が入るのでXの部分に[8][9]は入りません。
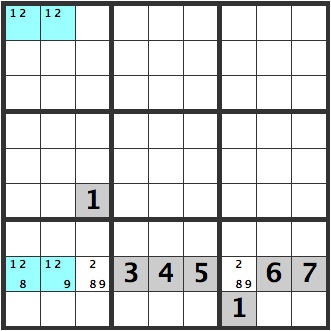
下の[128][129]のマスのどちらかに[8]か[9]が入るのですが、この行の他の空いている場所に[1]が入るマスがありません。ということで下の水色のマスのどちらかに[1]が入る必要がありますので、下段の水色マスに[2]を入れることはできません。
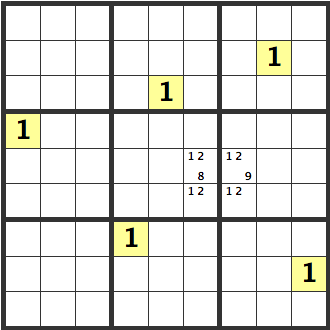
[128][129]のマスです。この行の空いているマスは全て[1]が入ることができないので、[128][129]のマスのどちらかに必ず[1]が入ることになり、[2]は候補から除外することができます。
NEXT:拡張ユニークレクタングル
| R1C1 | R1C2 | R1C3 | R1C4 | R1C5 | R1C6 | R1C7 | R1C8 | R1C9 |
| R2C1 | R2C2 | R2C3 | R2C4 | R2C5 | R2C6 | R2C7 | R2C8 | R2C9 |
| R3C1 | R3C2 | R3C3 | R3C4 | R3C5 | R3C6 | R3C7 | R3C8 | R3C9 |
| R4C1 | R4C2 | R4C3 | R4C4 | R4C5 | R4C6 | R4C7 | R4C8 | R4C9 |
| R5C1 | R5C2 | R5C3 | R5C4 | R5C5 | R5C6 | R5C7 | R5C8 | R5C9 |
| R6C1 | R6C2 | R6C3 | R6C4 | R6C5 | R6C6 | R6C7 | R6C8 | R6C9 |
| R7C1 | R7C2 | R7C3 | R7C4 | R7C5 | R7C6 | R7C7 | R7C8 | R7C9 |
| R8C1 | R8C2 | R8C3 | R8C4 | R8C5 | R8C6 | R8C7 | R8C8 | R8C9 |
| R9C1 | R9C2 | R9C3 | R9C4 | R9C5 | R9C6 | R9C7 | R9C8 | R9C9 |
Rは行(Y軸)、Cは列(X軸)となっています。(Row、Column)
 文章:
文章:DTP関連のIT技術者。システム開発など
運営:嵐山デザインガレージ合同会社