

Sponsored Links
TOP > Techniques > Aligned Pair Exclusion
Solving Techniques 19
Aligned Pair Exclusion
Please have a look below. We have the blue cells [4,8][2,8], which are strongly related to the pink cells [2,4][2,5,8].
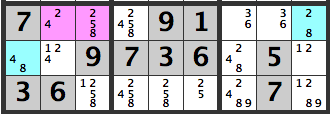
The possible combinations of the two pink cells are.
[2][2]
[2][5]
[2][8]
[4][2]
[4][5]
[4][8]
The combination of [2][2] is impossible.
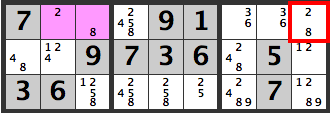
The [2][8] combination can’t be used because [R1C9]’s candidate is [2,8].
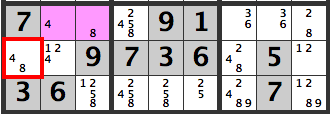
The [4,8] combination can’t be used because [R2C1]’s candidate is [4,8]. Hence we have,
[2][2]
[2][5]
[2][8]
[4][2]
[4][5]
[4][8]
and [8] can’t be entered in [R3C1].
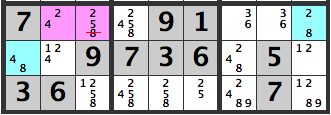
As seen above, the Aligned Pair Exclusion technique, considers all possible combinations between two cells to narrow down the candidates.
Aligned Pair Exclusion 2
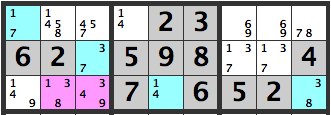
Here is another sample. Lets examine the pink cells in the diagram above. The combinations are
[1][3]
[1][4]
[1][9]
[3][3]
[3][4]
[3][9]
[8][3]
[8][4]
[8][9]
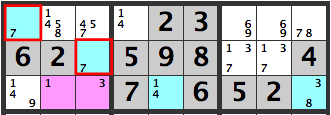
If the pink cells are [1][3], then the blue cells in the same box will be [7][7], which won’t work out.

If the pink cells are [1][4], then the blue cell in [R5C3]’s candidate will be [1,4], which won’t work out.
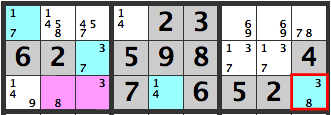
If the pink cels are [3][8], the candidates in the blue cell, [R9C3], will be [3,8], which won’t work out.
[1][3]
[1][4]
[1][9]
[3][3]
[3][4]
[3][9]
[8][3]
[8][4]
[8][9]
Hence, a [3] can’t be entered to the right of the pink boxes.
Sponsored Links
Aligned Pair Exclusion 3
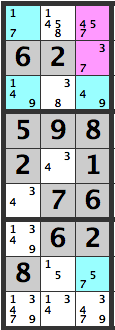
Here is another sample. Lets examine the pink cells in the diagram above. The combinations are:
[4][3]
[4][7]
[5][3]
[5][7]
[7][3]
[7][7]
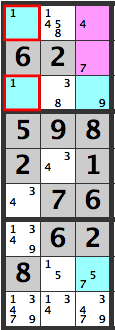
If the pink cells are [4][7], then the same box’s blue cells will become [1][1], which won’t work out.
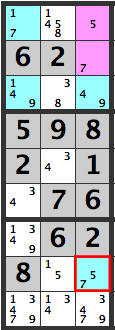
If the pink cells are [5][7], then the blue cell in [R3C8]’s candidates will be [5,7] which won’t work out.
[4][3]
[4][7]
[5][3]
[5][7]
[7][3]
[7][7]
Therefore, a [7] can’t be entered below the pink cells, so a [3] is confirmed here.
Aligned Pair Exclusion 4
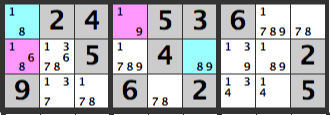
Here is another sample. Lets examine the pink cells in the diagram above. The combinations are:
[1][1]
[1][6]
[1][8]
[9][1]
[9][6]
[9][8]
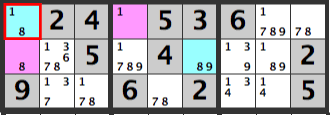
If the pink cells are [1][8], the candidates in the blue cell, [R1C1], will be [1,8], which won’t work out.
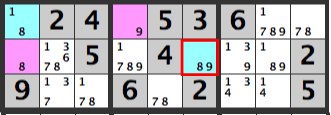
If the pink cells are [9][8], the candidates in the blue cell, [R6C2], will be [8,9], which won’t work out.
[1][1]
[1][6]
[1][8]
[9][1]
[9][6]
[9][8]
Hence, an [8] can’t be entered below the pink cells.
Aligned Pair Exclusion 5

Here is another sample. Lets examine the pink cells in the diagram above. The combinations are:
[1][4]
[1][5]
[1][7]
[2][4]
[2][5]
[2][7]
[7][4]
[7][5]
[7][7]

If the pink cells are [1][4], the candidates for the blue cell, [R9C2], will be [1,4], which won’t work out.

If the pink cells are [1][5], the candidates for the blue cell, [R8C2], will be [1,5], which won’t work out.

If the pink cells are [1][7], the candidates in both the blue cells [R1C3] and [R3C3] will be [9], which won’t work out.
[1][4]
[1][5]
[1][7]
[2][4]
[2][5]
[2][7]
[7][4]
[7][5]
[7][7]
Hence, a [1] can’t be entered to the left of the pink cells.
Names of cells in Sudoku
| R1C1 | R1C2 | R1C3 | R1C4 | R1C5 | R1C6 | R1C7 | R1C8 | R1C9 |
| R2C1 | R2C2 | R2C3 | R2C4 | R2C5 | R2C6 | R2C7 | R2C8 | R2C9 |
| R3C1 | R3C2 | R3C3 | R3C4 | R3C5 | R3C6 | R3C7 | R3C8 | R3C9 |
| R4C1 | R4C2 | R4C3 | R4C4 | R4C5 | R4C6 | R4C7 | R4C8 | R4C9 |
| R5C1 | R5C2 | R5C3 | R5C4 | R5C5 | R5C6 | R5C7 | R5C8 | R5C9 |
| R6C1 | R6C2 | R6C3 | R6C4 | R6C5 | R6C6 | R6C7 | R6C8 | R6C9 |
| R7C1 | R7C2 | R7C3 | R7C4 | R7C5 | R7C6 | R7C7 | R7C8 | R7C9 |
| R8C1 | R8C2 | R8C3 | R8C4 | R8C5 | R8C6 | R8C7 | R8C8 | R8C9 |
| R9C1 | R9C2 | R9C3 | R9C4 | R9C5 | R9C6 | R9C7 | R9C8 | R9C9 |
Sponsored Links


