Sudoku Kyo free sudoku game

Sponsored Links

TOP > Techniques > XYZ-Wing

Solving Techniques 10
XYZ-Wing

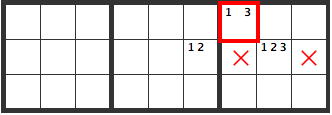
The XYZ-Wing is different from XY, in that three numbers are used. It is like the diagram below. When a problem turns out like this, a 3 will be entered somewhere.

If a 3 is entered in [R1C2], then it can’t be in the cells marked X, as shown below.

If a 3 is entered in [R1C5], then it can’t be in the cells marked X, as shown below.

If a 3 is entered in [R2C3], then it can’t be in the cells marked X, as shown below.

As you can see below, in the overlapping areas, X, a 3 can’t be entered.

Sponsored Links

Below is another XYZ wing, but not using [123] candidates, but rather a combination of three types of candidates, [12][23] and [13].

If a 3 is entered in [R2C3], it can’t be entered in the cells marked X, as shown below.

If a 3 is entered in [R1C5], it can’t be entered in the cells marked X, as shown below.

Hence, in the overlapping areas marked X, a 3 can’t be entered, as shown below. There are more X’s than in the previous example.

The numbers can also be further apart, as shown below. As in the previous examples, 3’s can’t be entered where the X’s are.

They can also be close together, as shown below. In this case, the common number is [1], so 1 can’t be entered in the cells with X’s.

This technique is an application of the XY-wing technique, so it seems to be easy to learn.

Names of cells in Sudoku

R1C1R1C2R1C3R1C4R1C5R1C6R1C7R1C8R1C9
R2C1R2C2R2C3R2C4R2C5R2C6R2C7R2C8R2C9
R3C1R3C2R3C3R3C4R3C5R3C6R3C7R3C8R3C9
R4C1R4C2R4C3R4C4R4C5R4C6R4C7R4C8R4C9
R5C1R5C2R5C3R5C4R5C5R5C6R5C7R5C8R5C9
R6C1R6C2R6C3R6C4R6C5R6C6R6C7R6C8R6C9
R7C1R7C2R7C3R7C4R7C5R7C6R7C7R7C8R7C9
R8C1R8C2R8C3R8C4R8C5R8C6R8C7R8C8R8C9
R9C1R9C2R9C3R9C4R9C5R9C6R9C7R9C8R9C9

Sponsored Links

Sudoku Kyoto（Number Place）Free Puzzle Game
TOP