

Sponsored Links
TOP > Techniques > Hidden Singles
Solving Techniques 1
Hidden Singles
Finding the last remaining number based on already confirmed numbers is very simple and it's the most basic technique used in Sudoku.
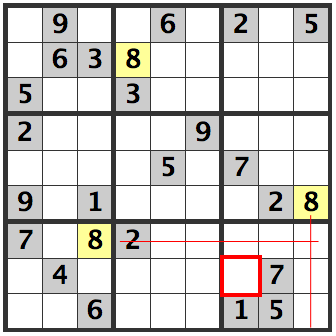
BOX
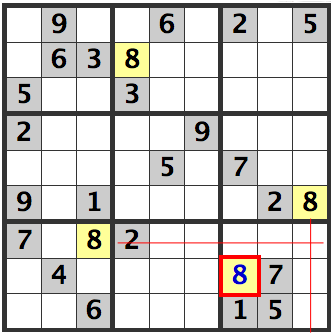
8's are already filled in as candidates in the [R7C3] and [R6C9] cells. This means that in the lower right hand box, an 8 is in the [R8C7] cell.
Line
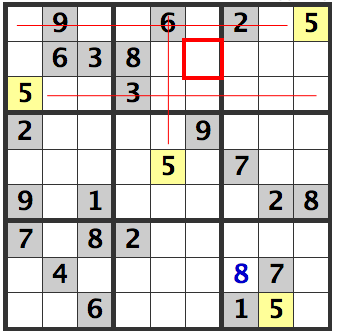
In the [2] Line, there are no 5's. In the upper left and upper right boxes, there are already confirmed 5's, which leaves [R2C5] and [R2C6] as the only options. Since there is already a 5 in [R5C5], the number 5 can't be in column 5, hence confirming that it is in [R2C6].
Sponsored Links
Line
Likewise, for [R5C6], there are 2's in rows [4] and [6] and since there is a 2 in column 4, the 2 is therefore in [R5C6], in the center block.
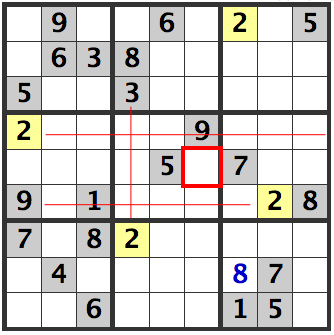
The hidden singles technique is a basic method to solve Sudoku problems.
This method of eliminating potential numbers in cells for rows, columns and boxes, until the last possible number remains, is at the foundation of Sudoku and it will be used at all levels.
Most of the beginning level problems on this site can be solved, solely using this method.
Names of cells in Sudoku
| R1C1 | R1C2 | R1C3 | R1C4 | R1C5 | R1C6 | R1C7 | R1C8 | R1C9 |
| R2C1 | R2C2 | R2C3 | R2C4 | R2C5 | R2C6 | R2C7 | R2C8 | R2C9 |
| R3C1 | R3C2 | R3C3 | R3C4 | R3C5 | R3C6 | R3C7 | R3C8 | R3C9 |
| R4C1 | R4C2 | R4C3 | R4C4 | R4C5 | R4C6 | R4C7 | R4C8 | R4C9 |
| R5C1 | R5C2 | R5C3 | R5C4 | R5C5 | R5C6 | R5C7 | R5C8 | R5C9 |
| R6C1 | R6C2 | R6C3 | R6C4 | R6C5 | R6C6 | R6C7 | R6C8 | R6C9 |
| R7C1 | R7C2 | R7C3 | R7C4 | R7C5 | R7C6 | R7C7 | R7C8 | R7C9 |
| R8C1 | R8C2 | R8C3 | R8C4 | R8C5 | R8C6 | R8C7 | R8C8 | R8C9 |
| R9C1 | R9C2 | R9C3 | R9C4 | R9C5 | R9C6 | R9C7 | R9C8 | R9C9 |
Sponsored Links

